QuantLib 아키텍처와 설계 철학
QuantLib-Python | QuantLib | 2025.04.12
1️⃣ QuantLib의 객체 지향 설계 원칙
QuantLib은 금융 애플리케이션을 위한 강력한 오픈 소스 라이브러리로, 잘 설계된 객체 지향 아키텍처를 기반으로 합니다. 이러한 설계는 복잡한 금융 개념을 명확하게 모델링하고, 코드의 재사용성과 확장성을 극대화하는 데 기여합니다.
✅ 핵심 설계 원칙
QuantLib은 다음과 같은 객체 지향 설계 원칙을 따릅니다:
추상화(Abstraction)
- 복잡한 금융 개념과 제품을 이해하기 쉬운 클래스로 추상화합니다. 예를 들어, 모든 금융 상품은
Instrument추상 클래스를 상속받아 구현됩니다. 이를 통해 개발자는 구체적인 구현 세부 사항보다 상품의 특성에 집중할 수 있습니다.
# 추상화의 예:
# 모든 금융 상품은 NPV(순현재가치) 계산 기능을 가집니다
instrument = some_financial_instrument
# 구체적인 구현과 관계없이 동일한 인터페이스
price = instrument.NPV()캡슐화(Encapsulation)
- 각 클래스는 자신의 데이터와 기능을 내부에 캡슐화하고, 잘 정의된 인터페이스를 통해서만 접근할 수 있게 합니다. 이는 코드의 안정성을 높이고 변경 시 영향을 최소화합니다.
상속(Inheritance)
- 기본 클래스에서 파생 클래스로 속성과 메서드를 상속함으로써 코드 재사용성을 높입니다. 예를 들어, 모든 옵션 유형은
Option클래스를 상속받아 공통 속성과 메서드를 공유합니다.
다형성(Polymorphism)
- 동일한 인터페이스를 통해 다양한 구현을 지원합니다. 이를 통해 다양한 금융 모델과 방법론을 유연하게 적용할 수 있습니다.
# 다형성의 예:
# 다양한 가격 책정 엔진을 동일한 인터페이스로 사용
option.setPricingEngine(analytic_engine) # 해석적 방법
option.setPricingEngine(monte_carlo_engine) # 몬테카를로 방법
option.setPricingEngine(binomial_tree_engine) # 이항 트리 방법✅ 모듈성과 확장성
QuantLib은 모듈화된 구조를 통해 확장성을 제공합니다. 새로운 금융 상품, 모델, 알고리즘을 기존 프레임워크에 쉽게 통합할 수 있습니다. 이는 금융 시장의 빠른 변화와 혁신에 대응하기 위한 중요한 특성입니다.
2️⃣ 주요 디자인 패턴
QuantLib은 여러 디자인 패턴을 활용하여 금융 애플리케이션의 복잡성을 관리합니다. 가장 중요한 패턴 몇 가지를 살펴보겠습니다.
✅ Observer/Observable 패턴
금융 시장 데이터는 지속적으로 변화하며, 한 데이터의 변경이 여러 계산에 영향을 미칩니다. QuantLib은 Observer/Observable 패턴을 사용하여 이러한 의존성을 관리합니다.
- Observable: 관찰 가능한 객체로, 상태가 변경되면 등록된 모든 Observer에게 알림을 보냅니다.
- Observer: Observable 객체를 관찰하고, 변경 알림을 받으면 자신의 상태를 업데이트합니다.
import QuantLib as ql
# SimpleQuote는 Observable의 일종입니다
spot_price = ql.SimpleQuote(100.0)
# 이 가격에 의존하는 다른 객체들이 Observer로 등록됩니다
# 가격 변경 시 자동으로 업데이트됩니다
# 값 변경 시 모든 의존 객체에 알림이 전달됩니다
spot_price.setValue(105.0)이 패턴은 금융 모델에서 특히 유용합니다. 예를 들어, 기초 자산 가격이 변경되면 이에 의존하는 모든 파생상품 가격이 자동으로 업데이트됩니다.
✅ Handle/Quote 패턴
QuantLib은 금융 시장 데이터를 유연하게 관리하기 위해 Handle/Quote 패턴을 사용합니다.
- Quote: 시장 데이터(예: 주가, 금리, 변동성)를 나타내는 인터페이스
- Handle: Quote에 대한 참조를 저장하는 래퍼(wrapper) 클래스로, 런타임에 참조 대상을 변경할 수 있음
import QuantLib as ql
# 시장 데이터 생성
spot_price = ql.SimpleQuote(100.0)
spot_handle = ql.QuoteHandle(spot_price)
# 핸들을 사용하여 객체 생성
process = ql.BlackScholesProcess(spot_handle, ...)
# 나중에 참조 대상을 변경하지 않고 기초 데이터 업데이트 가능
spot_price.setValue(105.0) # 자동으로 process에 반영됨이 패턴은 시장 데이터의 실시간 업데이트를 처리하거나, 동일한 모델에 다른 시장 시나리오를 적용할 때 유용합니다.
✅ LazyObject 패턴
금융 계산은 종종 계산 비용이 높습니다. QuantLib은 LazyObject 패턴을 사용하여 필요할 때만 계산을 수행하는 지연 평가(lazy evaluation)를 구현합니다.
- LazyObject: 실제로 필요할 때까지 계산을 지연시키고, 의존하는 데이터가 변경될 때만 재계산하는 객체
# YieldTermStructure는 LazyObject를 상속받습니다
# 내부 계산은 실제로 금리가 필요할 때만 수행됩니다
rate = yield_curve.zeroRate(5.0, ql.Continuous)이 패턴은 복잡한 수익률 곡선이나 변동성 표면과 같이 계산 비용이 높은 객체에 특히 유용합니다.
✅ 팩토리 패턴
QuantLib은 다양한 금융 객체의 생성을 관리하기 위해 팩토리 패턴을 사용합니다.
- 팩토리: 객체 생성 로직을 캡슐화하여, 클라이언트 코드에서 구체적인 클래스 대신 인터페이스를 다룰 수 있게 합니다.
# 옵션 팩토리의 예시
# (QuantLib에서 명시적으로 팩토리 클래스를 제공하지는 않지만,
# 많은 생성 패턴이 이 개념을 따름)
engine = ql.MakeFdBlackScholesVanillaEngine(process)
.withTGrid(100)
.withXGrid(100)
.withCashDividendModel()3️⃣ 클래스 계층 구조 개요
QuantLib은 금융 개념을 모델링하기 위한 풍부한 클래스 계층 구조를 제공합니다. 주요 계층 구조를 살펴보겠습니다.
✅ 금융 상품 계층 구조
모든 금융 상품은 Instrument 추상 클래스에서 파생됩니다:
Instrument
├── Option
│ ├── VanillaOption
│ ├── ExoticOption
│ │ ├── BarrierOption
│ │ ├── AsianOption
│ │ └── ...
│ └── ...
├── Bond
│ ├── ZeroCouponBond
│ ├── FixedRateBond
│ ├── FloatingRateBond
│ └── ...
├── Swap
│ ├── VanillaSwap
│ ├── CrossCurrencySwap
│ └── ...
└── ...이러한 계층 구조는 공통 기능을 상위 클래스에 구현하고, 특정 상품의 차별화된 특성을 하위 클래스에 구현함으로써 코드 재사용성을 극대화합니다.
✅ 시장 데이터 구조
시장 데이터는 다음과 같은 계층 구조로 구성됩니다:
TermStructure
├── YieldTermStructure
│ ├── FlatForward
│ ├── PiecewiseYieldCurve
│ └── ...
├── VolatilityTermStructure
│ ├── BlackConstantVol
│ ├── BlackVarianceSurface
│ └── ...
└── DefaultTermStructure
├── FlatHazardRate
├── PiecewiseDefaultCurve
└── ...이러한 구조는 다양한 시장 데이터를 일관된 인터페이스로 접근할 수 있게 해줍니다.
✅ 가격 책정 엔진
가격 책정 엔진은, 금융 상품의 가격을 계산하는 알고리즘을 구현합니다:
PricingEngine
├── VanillaOptionEngine
│ ├── AnalyticEuropeanEngine
│ ├── BinomialVanillaEngine
│ ├── MCEuropeanEngine
│ └── ...
├── BondEngine
│ ├── DiscountingBondEngine
│ └── ...
└── ...이 설계는 동일한 금융 상품을 다양한 방법론으로 가격 책정할 수 있게 합니다.
4️⃣ Python 바인딩의 특징
QuantLib은 원래 C++로 작성되었지만, QuantLib-Python을 통해 Python에서도 사용할 수 있습니다. Python 바인딩은 몇 가지 특징을 가지고 있습니다.
✅ SWIG를 통한 인터페이스
QuantLib-Python은 SWIG(Simplified Wrapper and Interface Generator)를 사용하여 C++ 코드를 Python으로 래핑합니다. 이를 통해 C++ 클래스와 함수가 Python 모듈로 노출됩니다.
✅ C++와 Python의 차이점
Python 인터페이스는 C++ 라이브러리와 거의 동일하지만, 몇 가지 차이점이 있습니다:
- 네이밍 규칙: C++의 camelCase 대신 Python에서는 일부 메서드가 snake_case 규칙을 따르기도 합니다.
- 연산자 오버로딩: Python에서는 일부 C++ 연산자 오버로딩이 다르게 구현됩니다.
- 메모리 관리: Python의 가비지 컬렉션이 C++ 객체의 수명을 관리합니다.
✅ Python 사용 시 장점
Python은 금융 분석에 인기 있는 언어이며, QuantLib-Python을 사용하면 다음과 같은 장점이 있습니다:
- 쉬운 학습 곡선: Python은 C++보다 배우기 쉽고, 더 간결한 문법을 제공합니다.
- 데이터 과학 생태계 통합: NumPy, pandas, matplotlib과 같은 데이터 과학 라이브러리와 쉽게 통합됩니다.
- 빠른 프로토타이핑: Python은 개발 속도가 빨라 금융 모델을 빠르게 프로토타이핑하기에 적합합니다.
# Python 통합 예시
import QuantLib as ql
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# QuantLib 계산 수행
spot_prices = np.linspace(80, 120, 41)
option_prices = []
for spot in spot_prices:
# 기초자산가격 설정
spot_quote.setValue(spot)
# 계산 수행, european_option:
# 이전 페이지 예제에서 만든 객체
option_prices.append(european_option.NPV())
# Pandas와 Matplotlib을 사용한 결과 분석
df = pd.DataFrame({'SpotPrice': spot_prices,
'OptionPrice': option_prices})
plt.figure(figsize=(10, 6))
plt.plot(df['SpotPrice'], df['OptionPrice'])
plt.title('Option Price vs. Spot Price')
plt.xlabel('Spot Price')
plt.ylabel('Option Price')
plt.grid(True)
plt.show()# 출력 결과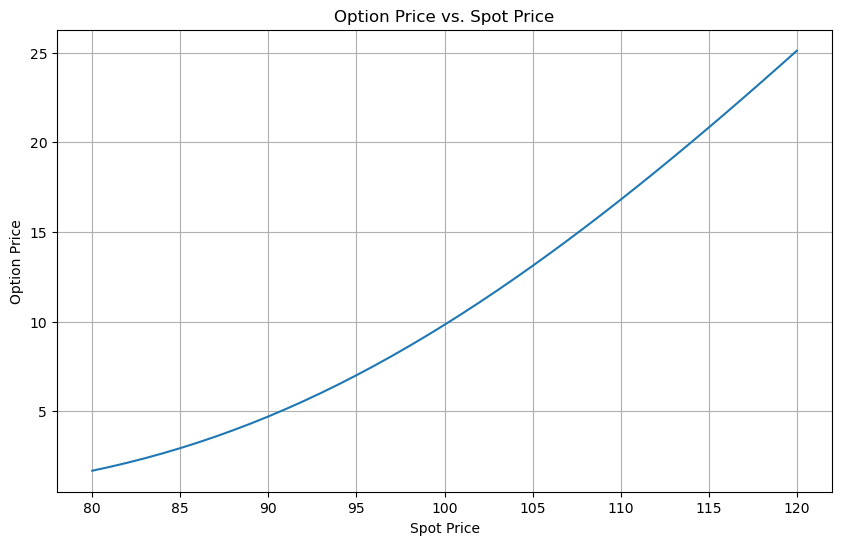
5️⃣ 예제: 기본 객체 생성 및 상호작용
QuantLib의 아키텍처를 더 잘 이해하기 위해 간단한 예제를 통해 주요 객체 간의 상호작용을 살펴보겠습니다. 이 예제에서는 유럽형 콜옵션을 가격 책정하는 기본 프로세스를 구현합니다.
import QuantLib as ql
# 1. 날짜 설정
valuation_date = ql.Date(15, 1, 2025)
ql.Settings.instance().evaluationDate = valuation_date
maturity_date = ql.Date(15, 1, 2026) # 1년 만기
# 2. 시장 데이터 설정 (Observable 객체)
spot_price = ql.SimpleQuote(100.0) # 기초자산 가격
risk_free_rate = ql.SimpleQuote(0.05) # 무위험 이자율
volatility = ql.SimpleQuote(0.2) # 변동성
# 3. Handle 생성 (인터페이스 추상화)
spot_handle = ql.QuoteHandle(spot_price)
rate_handle = ql.YieldTermStructureHandle(
ql.FlatForward(valuation_date,
ql.QuoteHandle(risk_free_rate),
ql.Actual365Fixed())
)
vol_handle = ql.BlackVolTermStructureHandle(
ql.BlackConstantVol(valuation_date,
ql.NullCalendar(),
ql.QuoteHandle(volatility),
ql.Actual365Fixed())
)
# 4. 프로세스 생성 (확률적 과정 모델링)
process = ql.BlackScholesProcess(spot_handle,
rate_handle,
vol_handle)
# 5. 옵션 설정 (상품 정의)
strike = 100.0
option_type = ql.Option.Call
payoff = ql.PlainVanillaPayoff(option_type, strike)
exercise = ql.EuropeanExercise(maturity_date)
option = ql.VanillaOption(payoff, exercise)
# 6. 가격 책정 엔진 설정 (계산 알고리즘 선택)
engine = ql.AnalyticEuropeanEngine(process)
option.setPricingEngine(engine)
# 7. 결과 계산
option_price = option.NPV()
option_delta = option.delta()
option_gamma = option.gamma()
# QuantLib은 1% 변화에 대한 vega를 계산
option_vega = option.vega() / 100
print(f"옵션 가격: {option_price:.4f}")
print(f"델타: {option_delta:.4f}")
print(f"감마: {option_gamma:.6f}")
print(f"베가: {option_vega:.4f}")
# 8. 시장 데이터 변경 (Observer/Observable 패턴 시연)
print("\n기초자산 가격을 110으로 변경:")
# 이 변경은 자동으로 모든 의존 객체에 전파됩니다
spot_price.setValue(110.0)
# 결과 재계산 (지연 평가 - 필요할 때만 계산됨)
print(f"옵션 가격: {option.NPV():.4f}")
print(f"델타: {option.delta():.4f}")# 출력 결과
# 옵션 가격: 10.4506
# 델타: 0.6368
# 감마: 0.018762
# 베가: 0.3752
# 기초자산 가격을 110으로 변경:
# 옵션 가격: 17.6630
# 델타: 0.7958이 예제는 QuantLib의 주요 아키텍처 특성을 보여줍니다:
- 객체 지향 설계: 각 금융 개념(날짜, 시장 데이터, 상품, 엔진)이 독립적인 클래스로 모델링됩니다.
- Observer/Observable 패턴: 시장 데이터 변경이 자동으로 모든 의존 객체에 전파됩니다.
- Handle/Quote 패턴: 시장 데이터에 대한 참조가 추상화됩니다.
- 지연 평가: 결과는 필요할 때만 계산됩니다.
6️⃣ 실제 응용: 다양한 가격 책정 방법 비교
금융 모델링에서는 동일한 상품을 여러 방법으로 가격 책정하는 것이 일반적입니다. QuantLib의 유연한 아키텍처는 이를 쉽게 구현할 수 있게 해줍니다.
import QuantLib as ql
import matplotlib.pyplot as plt
import numpy as np
import time
# 기본 설정 (앞서 예제와 동일)
valuation_date = ql.Date(15, 1, 2025)
ql.Settings.instance().evaluationDate = valuation_date
maturity_date = ql.Date(15, 1, 2026)
spot = ql.SimpleQuote(100.0)
rate = ql.SimpleQuote(0.05)
vol = ql.SimpleQuote(0.2)
spot_handle = ql.QuoteHandle(spot)
rate_handle = ql.YieldTermStructureHandle(
ql.FlatForward(valuation_date,
ql.QuoteHandle(rate),
ql.Actual365Fixed())
)
vol_handle = ql.BlackVolTermStructureHandle(
ql.BlackConstantVol(valuation_date,
ql.NullCalendar(),
ql.QuoteHandle(vol),
ql.Actual365Fixed())
)
process = ql.BlackScholesProcess(spot_handle,
rate_handle,
vol_handle)
# 옵션 설정
strike = 100.0
option_type = ql.Option.Call
payoff = ql.PlainVanillaPayoff(option_type, strike)
exercise = ql.EuropeanExercise(maturity_date)
option = ql.VanillaOption(payoff, exercise)
# 다양한 가격 책정 엔진 설정
# 1. 해석적 방법 (Black-Scholes 공식)
analytic_engine = ql.AnalyticEuropeanEngine(process)
# 2. 이항 트리 방법 (Cox-Ross-Rubinstein 모델)
binomial_engine = ql.BinomialVanillaEngine(process, "crr", 100)
# 3. 몬테카를로 시뮬레이션 방법
mc_engine = ql.MCEuropeanEngine(process, "pseudorandom",
timeSteps=100,
requiredSamples=10000,
seed=42)
# 각 방법으로 가격 계산 및 성능 측정
engines = [
("Black-Scholes Analytic Method", analytic_engine),
("Binomial Tree Method (100 Step)", binomial_engine),
("Monte Carlo Method (10,000)", mc_engine)
]
results = []
for name, engine in engines:
start_time = time.time()
option.setPricingEngine(engine)
price = option.NPV()
elapsed_time = time.time() - start_time
results.append({
"방법": name,
"가격": price,
"계산 시간(초)": elapsed_time
})
# 결과 출력
print("다양한 가격 책정 방법 비교:")
for result in results:
print(f"{result['방법']}: {result['가격']:.6f} (계산 시간: {result['계산 시간(초)']:.6f}초)")
# 행사가 변화에 따른 각 방법의 결과 비교
strikes = np.linspace(80, 120, 21)
prices = {name: [] for name, _ in engines}
for strike in strikes:
payoff = ql.PlainVanillaPayoff(option_type, strike)
option = ql.VanillaOption(payoff, exercise)
for name, engine in engines:
option.setPricingEngine(engine)
prices[name].append(option.NPV())
# 결과 시각화
plt.figure(figsize=(10, 6))
for name, _ in engines:
plt.plot(strikes, prices[name], label=name)
plt.title('Option Price by Strike Price')
plt.xlabel('Strike Price')
plt.ylabel('Option Price')
plt.legend()
plt.grid(True)
plt.show()# 출력 결과
# 다양한 가격 책정 방법 비교:
# Black-Scholes Analytic Method: 10.450584 (계산 시간: 0.000141초)
# Binomial Tree Method (100 Step): 10.429986 (계산 시간: 0.000076초)
# Monte Carlro Method (10,000): 10.526726 (계산 시간: 0.166369초)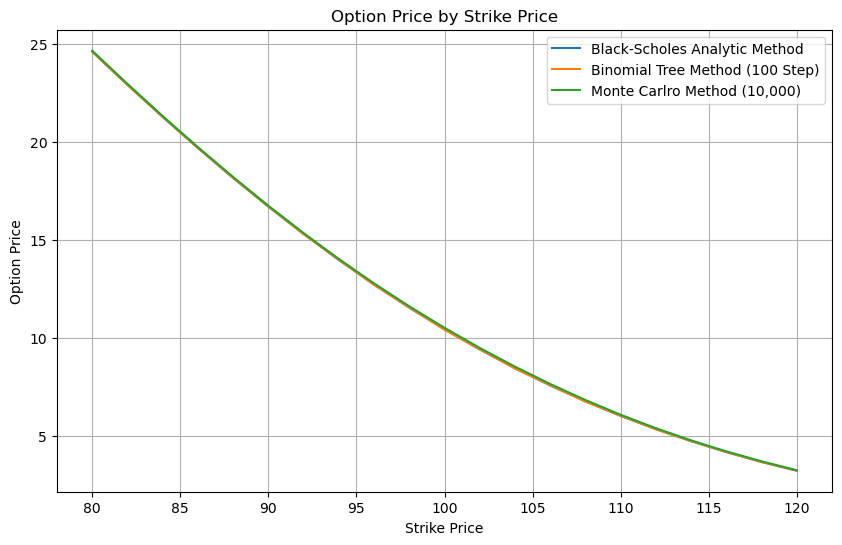
이 예제는 QuantLib의 아키텍처가 얼마나 유연한지 보여줍니다. 동일한 옵션을 다양한 방법론으로 가격 책정할 수 있으며, 각 방법의 결과와 성능을 비교할 수 있습니다.
7️⃣ 요약 및 다음 단계
이번 섹션에서는 QuantLib의 아키텍처와 설계 철학에 대해 살펴보았습니다. QuantLib은 객체 지향 설계 원칙을 따르며, Observer/Observable, Handle/Quote, LazyObject와 같은 디자인 패턴을 활용하여 금융 애플리케이션의 복잡성을 관리합니다. 이러한 아키텍처는 코드의 재사용성, 확장성, 유지보수성을 높이며, 다양한 금융 상품과 모델을 일관된 방식으로 구현할 수 있게 해줍니다.
Python 바인딩을 통해 QuantLib의 강력한 기능을 NumPy, pandas, matplotlib과 같은 데이터 과학 라이브러리와 쉽게 통합할 수 있으며, 이는 금융 분석 및 모델링 작업을 더욱 효율적으로 수행할 수 있게 해줍니다.
추가 학습 자료
- "Implementing QuantLib" by Luigi Ballabio (QuantLib의 주요 개발자)
- "C++ Design Patterns and Derivatives Pricing" by Mark S. Joshi
- QuantLib 공식 문서
- QuantLib GitHub 저장소